​

In order to optimize the productivity and cost efficiency of metallurgical processes and metallurgical plants, numerical tools are essential today and are already available in a great variety. Most metallurgical calculations, however, relate to specific individual process stages and only offer the possibility of only optimizing these offline. While these tools can be used to evaluate performance for a variety of process concepts, design criteria, input materials, energy use, and other process parameters, it is limited to individual process stages.

 

No previous simulation software can be applied consistently to all successive production steps and areas of a metallurgical production plant from the melt to the product. Of course, it would be desirable to use these tools both for the design of the metallurgical systems and for later operational online use. Online process models offer the possibility of transparent process management and support functions in decision-making processes. The metallurgists' vision, however, is an adaptive, integrated process model - from design and process optimization to online support. This is exactly the path we follow with our #EVA software

​

Basics for simulating processes from melting to the product

Digitization describes a holistic approach to networking. We understand the term networking to mean the expansion of connections between individual elements of a system. In the area of ​​"knowledge engineering" networking means linking fragments of knowledge to create new ideas. The digitization, i.e. digital networking of information, is mapped in relational databases.

The digitization includes the "data warehouse", “Predictive Maintenance”, “Deep Learning”, “Prediction Model” and “Parameter Fitting”.

 

• The “data warehouse”, as an additional “data layer”, enables sustainable digital networking and the homogenization of the model landscape. The good availability of data enables holistic production planning, quality control and, based on this, holistic quality optimization. The aim is to show a numerical model approach that is suitable for the holistic simulation of metallurgical processes (process chains) before and after the heat treatment. Selected examples in the field of metallurgical processes as well as heat treatment processes are presented.
   

• "Machine Learning": With the help of algorithms, data is analyzed and sorted for given questions. A distinction is made between supervised learning (forked data, i.e. white, e.g. color is green) and unguarded learning (the algorithm creates a picture for itself). The product of “machine learning” is often the “prediction model”.
   

• "Prediction Model": Essentially, these are the models created during "Machine Learning" that make it possible to call up a forecast, e.g. the probability of a machine condition. This forecast has a quality and a confidence interval that can be taken into account when using the forecast.
   

• "Predictive Maintenance": A discipline of "Machine Learning". With the help of all data e.g. of a machine, algorithms provide forecasts of when a machine component is subject to a condition (e.g. a defect). Roll bearings, for example, are monitored using FFT analyzes and damage can thus be detected at an early stage.
   

• "Deep-Learning": A special type of "Machine Learning" that essentially consists of the use of neural networks. With high computing power, e.g. Classification problems are resolved.
   

• “Parameter fitting”: Most calculation models have a set of dimensionless parameters for which empirical values ​​are available (so-called parameter models). In many cases, statistical calculations must be used to find suitable parameters in order to maintain the required quality of the forecast. The so-called fitting can be done through mathematical optimization, simple trial and error or through the use of "machine learning".

 

​

Business Intelligence Tools

• Visualization of data and content tailored to the user: The production manager will usually see balance sheets, statistics on production and failures. The machine operator sees data relating to his machine, machine M runs with failure rate A.
   

• Through the coupling with a "data warehouse" it is possible to view all data in a suitable way. Temporal progressions or distributions. Information in different ways can be compared with others, so that e.g. can identify sources of error by considering the reworking portion of a product across all possible influencing factors.
   

• Creation of reports (prefabricated and self-generated).

 

 

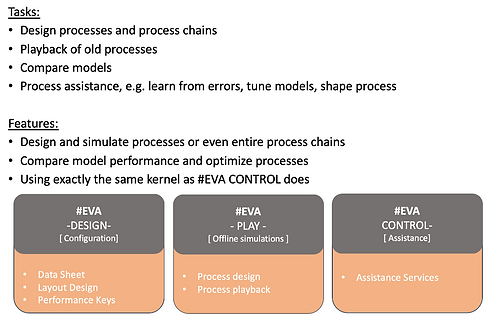
Assistant functions

The separation of metallurgical calculations and the HMI enables independent further development. At the same time, the architecture allows easy selection of the calculation results through the free definition of the equations (Assistant Function).

The numerical model core can be adapted to the individual needs of customers quickly and very cost-saving while the HMI remains independent.

 

​